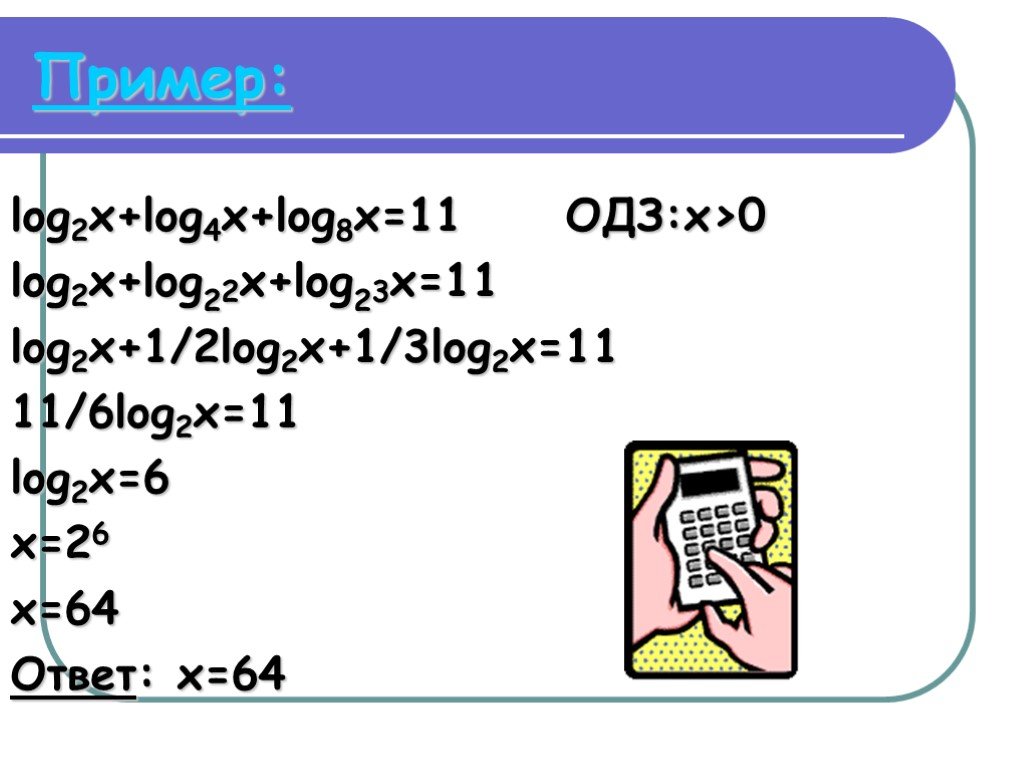
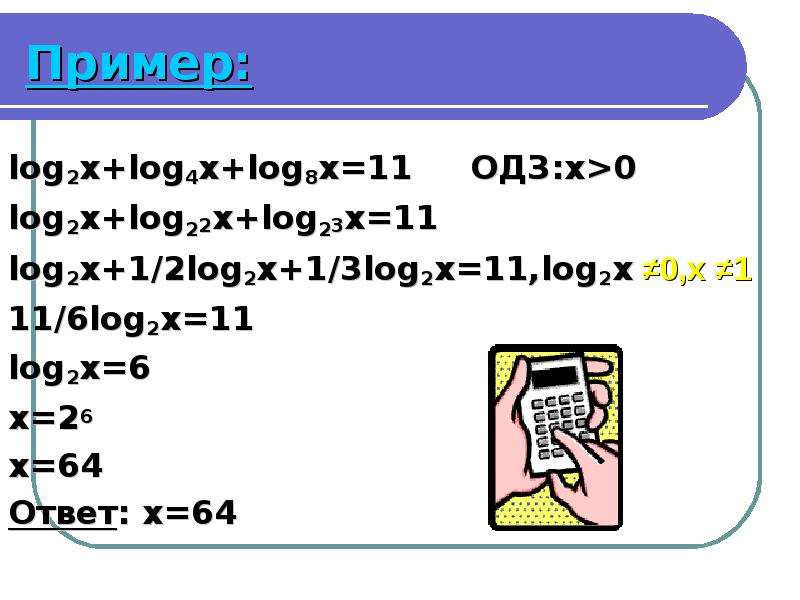
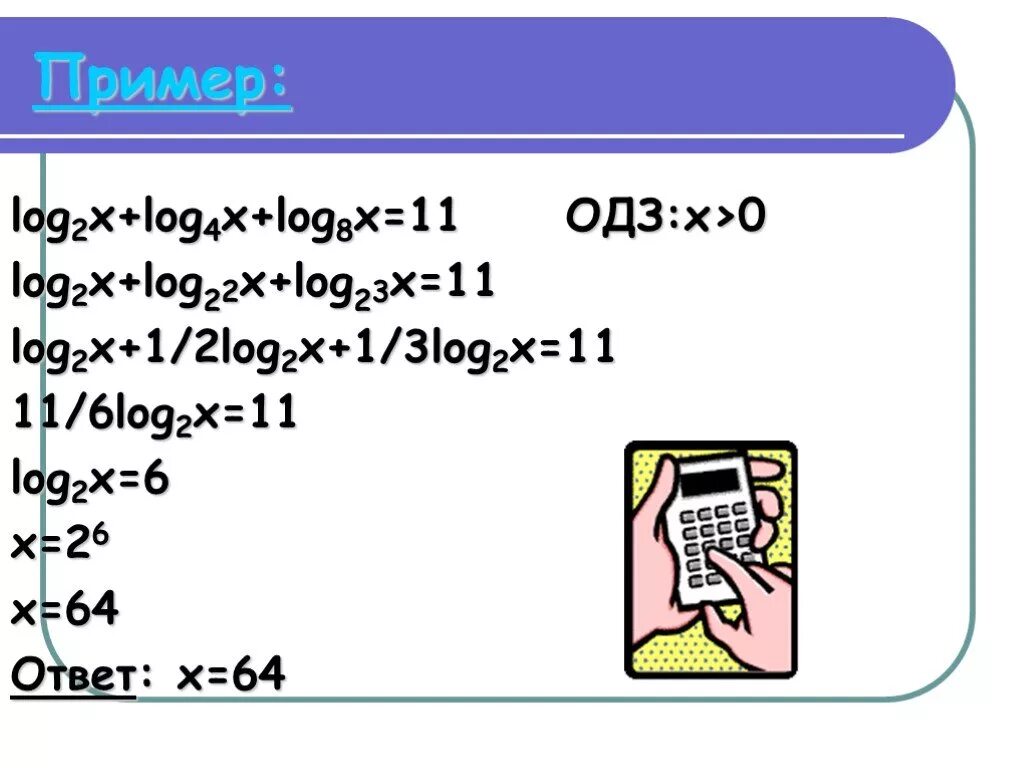
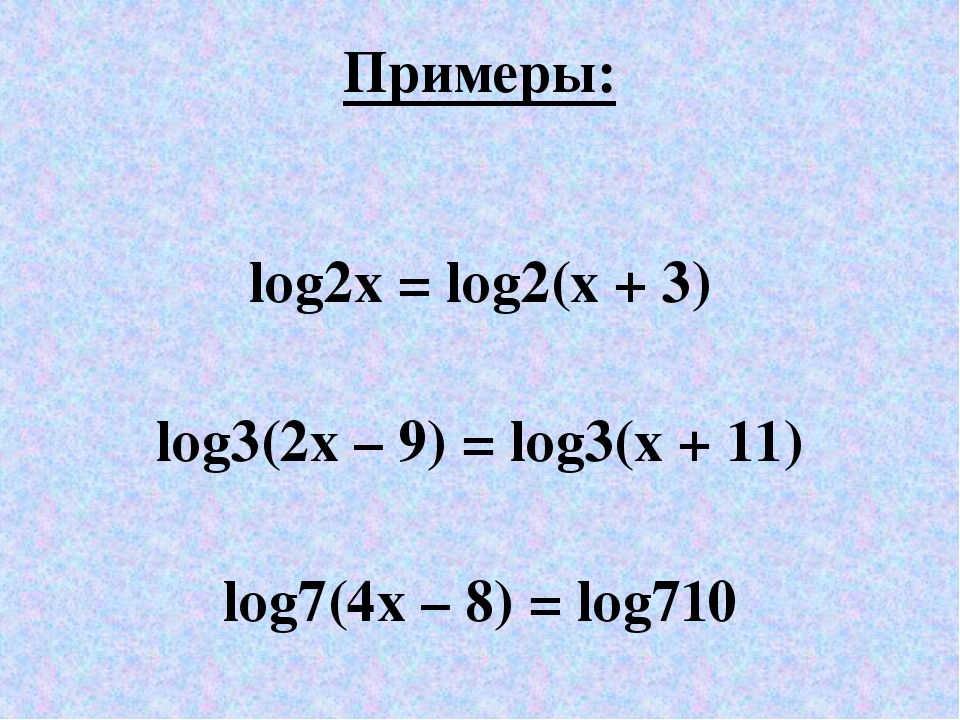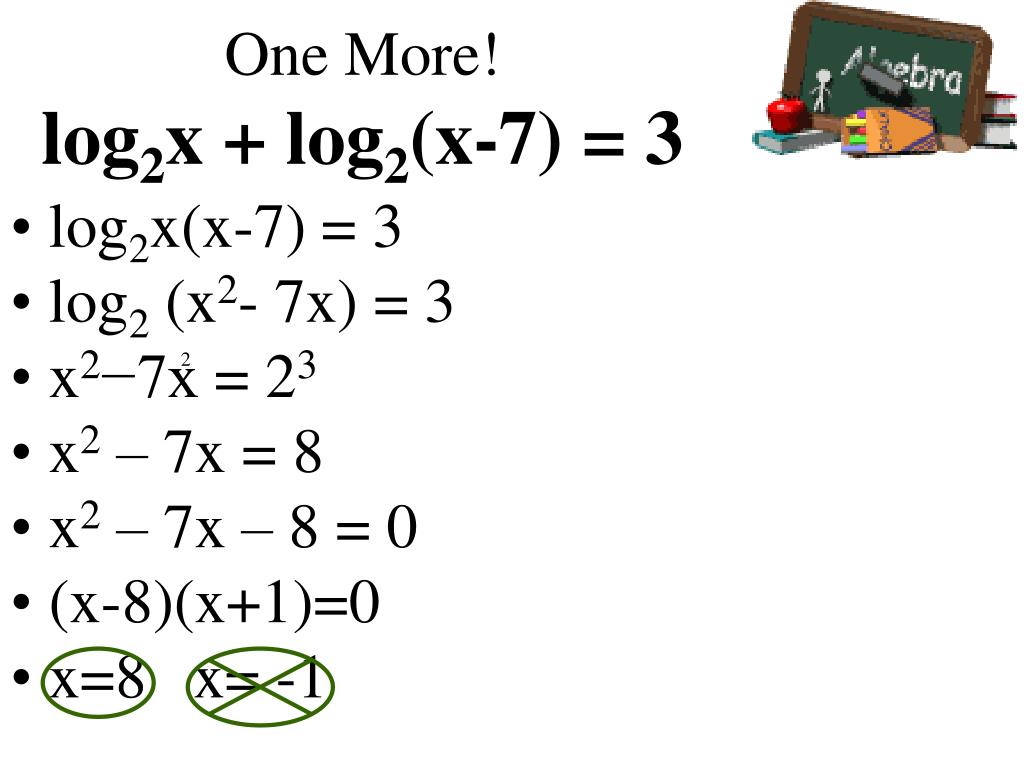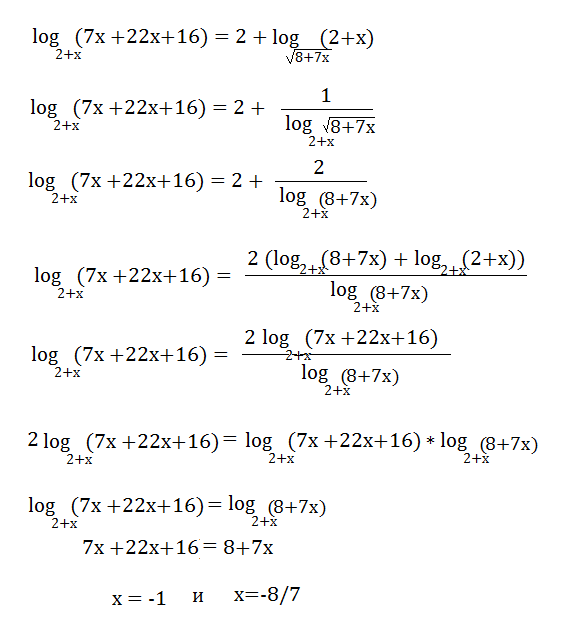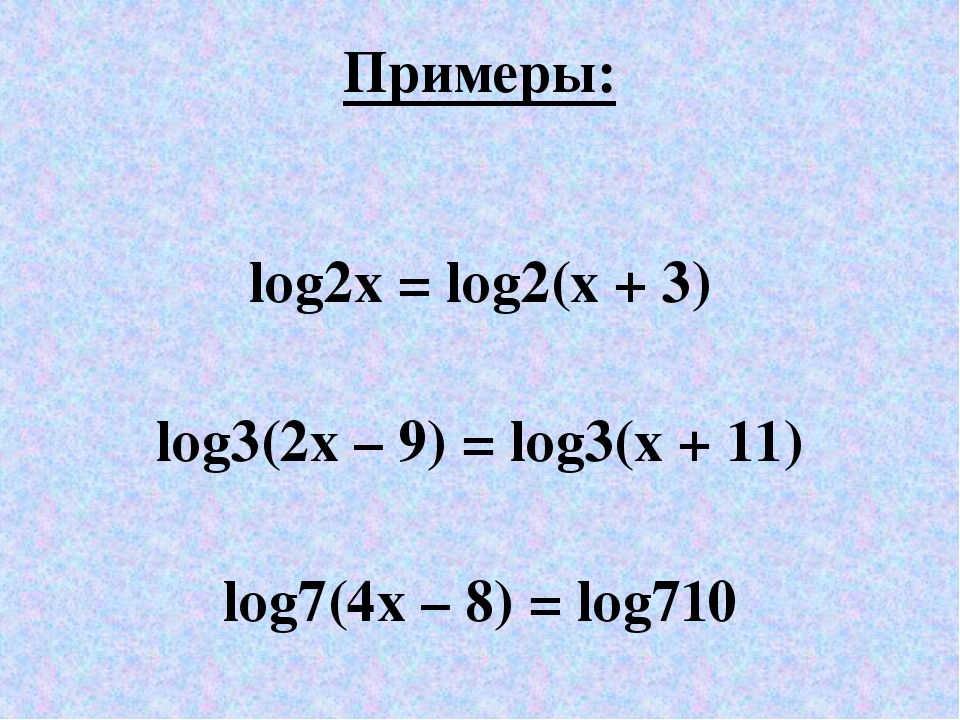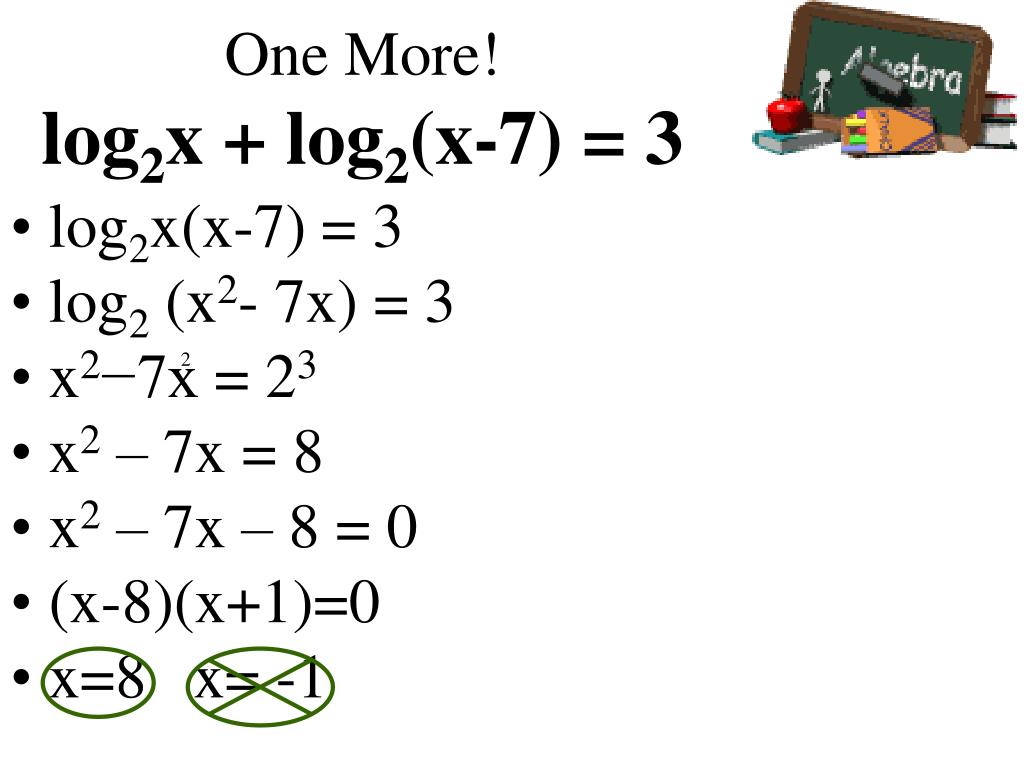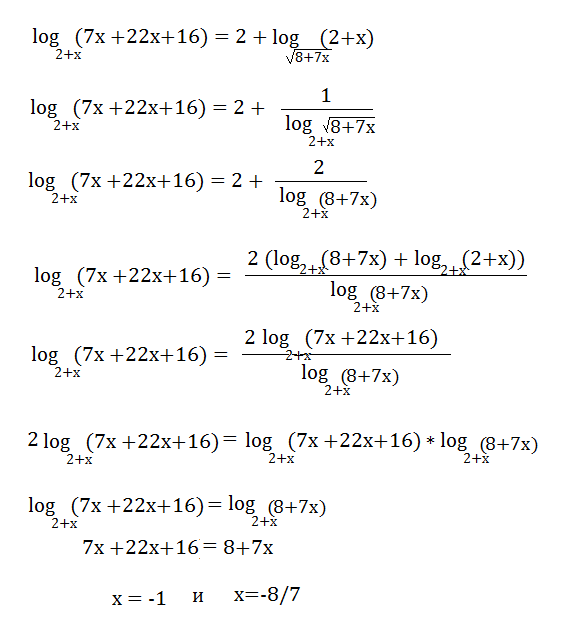Log5x=2. Метод введения новой переменной логарифмические уравнения. Log2(x-1)<1. Log2x log2. 2 log2 x 5 log.
|
Log2x log2. Лог 2. Log1/2(х2-4х-1). Log2x log2. Log2x log2.
|
Log2x=3. Log2 2. Log2x log2. У= лог2(x-3). Log^2 2 (x^2).
|
Log2 (2x+1)>1. Log2 х. Log2 0. Log2x. Log 0.
|
Log3(x-2)<2. Log 1/2 x. Log2x<1/2. 1-log2 x^2 + 2(log2 x)^2. Log2x log2.
|
Логарифм 9. Решить неравенство log _(2)(x+1)+log _(3)x<=3. Log2(1-x)+log2(3-x)=3. Log2 2. Log3(x+2)<3.
|
Log3 1/3. Log2x log2. Лог2(х+1) -3. Log2x log2. 2log5 -x log5 x+2.
|
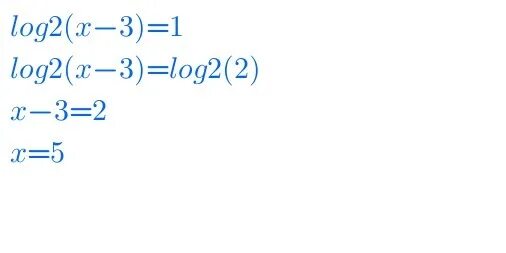Log 1/2 x. Log2x log2. Log2x log2. Решить уравнение log. Log2x log2.
|
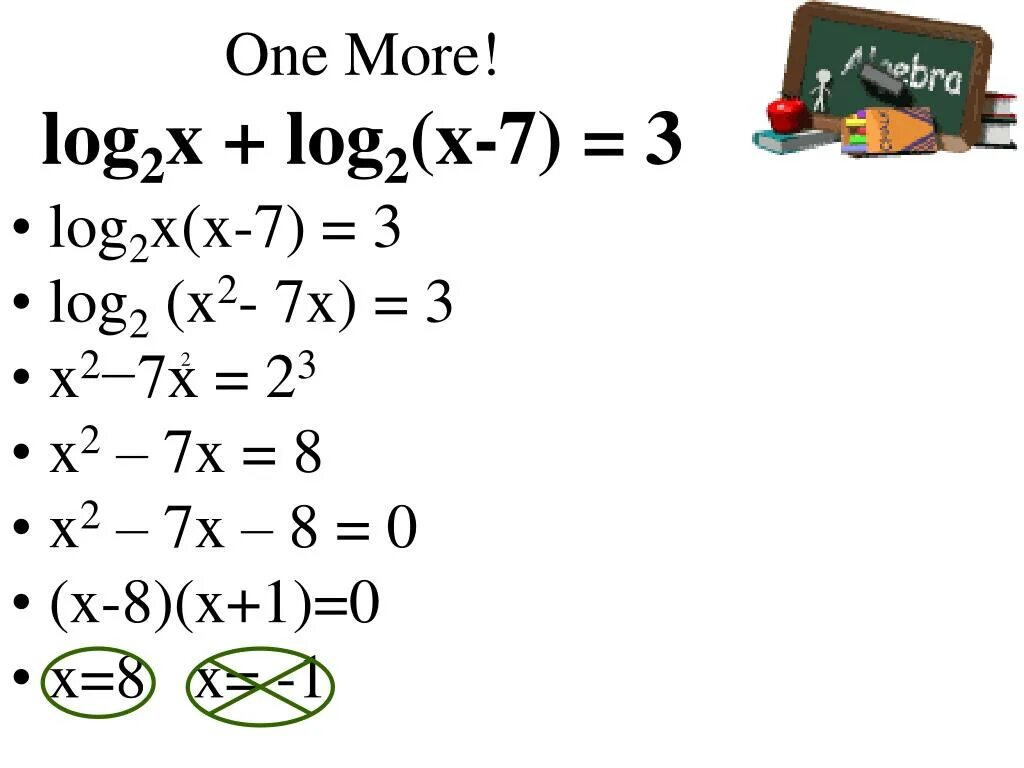Log2x log2. Log2. Log2x log2. Log10 0,01. Log2x=3.
|
Логарифмические уравнения log2/3 + log3. Log 1. Log 1/2 x. Log2x log2. Log 1/2 x.
|
Log2x log2. 5 log x 1 3 x 2 8 x 4 x 2 3 x 2 log x 1 25. Log3. Log2x log2. 2log23-1.
|
Log2x log2. Log2 x 2 4 3 log2 x+2/x-2. 2log2 3. Log2(x2-3x)=2. Log2 как решать.
|
Log2x x+4 logx 2-x. Log2(x+2)=5. Введение новой переменной логарифмических уравнений. I log2n. Log2x.
|
Log2x log2. Log 2 x = − x. Log2x<1/2. Log2x log2. Лог1/3 x > 4.
|
Log3. Log2. Log 1/2 x. Log 1/2 x. 2log2 3.
|
Log^2 2 (x^2). Log x x 1 2. Log решение. Logx = e^. Log 2 x = − x.
|
Log1/2(x+1) <- log2(2-x);. Решите неравенство log0 5 1-3x -2. Log2x log2. Лог1/3 x > 4. 4 решить неравенство log 1/3 (3−2 х )>−1.
|
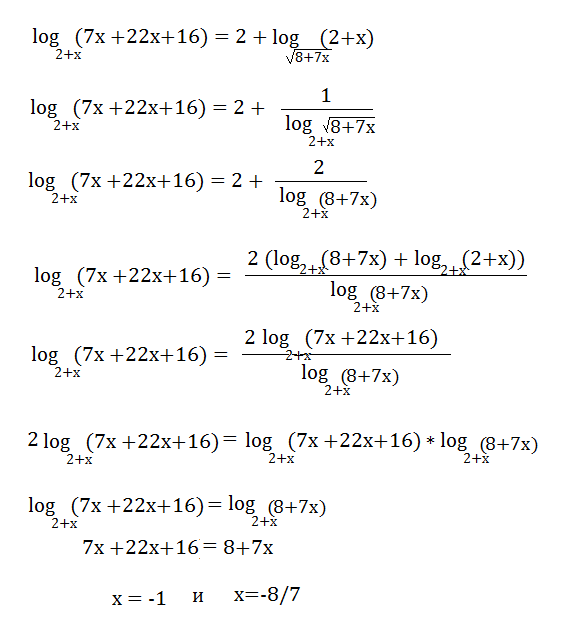2log9 x2+4x /log9x2 1. Log2x=3. Лог2(х+1) -3. Log3. Log1/2(х2-4х-1).
|
Log2x log2. Log3 1/3. Log2 2. Log3. 2log2 3.
|
Log2 как решать. Log1/2(х2-4х-1). Log2x log2. Log 2 x = − x. Log 1/2 x.
|
